Что такое сумма матриц

Действия с матрицами

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов:

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки:

и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: – матрица «три на три».

Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

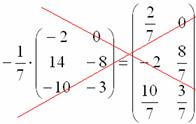
Сначала рассмотрим то, чего делать НЕ НАДО:

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Сначала переписываем первую строку в первый столбец:

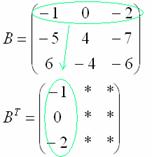
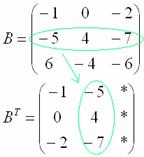
Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

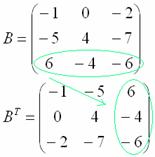
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

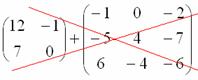
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
Можно ли умножить матрицу на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно:

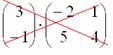
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:

– попытайтесь сразу уловить закономерность.

Умножить матрицу на матрицу

В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение (правильный ответ ).

Обратите внимание, что ! Это почти всегда так!

Таким образом, при умножении переставлять матрицы нельзя!

Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.

А пока спектакль закончен.

После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Zaochnik.com – профессиональная помощь студентам,

cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys

© Copyright mathprofi.ru, Александр Емелин, 2010-2022. Копирование материалов сайта запрещено

Математика для чайников. Матрицы и основные действия над ними

1-й курс, высшая математика, изучаем матрицы и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого — определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Элементы, для которых i=j (a11, a22, .. ) образуют главную диагональ матрицы, и называются диагональными.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы — A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот — столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис. Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.

Сложение матриц и вычитание матриц

Линейная алгебра

Рассмотрим в данной статье такие линейные операции над матрицами — сложение матриц. Дадим определение суммы матриц и приведем примеры на сложение матриц с подробным объяснением. Приведем свойства сложения матриц

Сложение матриц

Сумма матриц A и B — это матрица C, в которой все элементы есть суммы соответствующих элементов матриц A и B. При этом сами матрицы должны иметь одинаковое строение — или быть прямоугольными типа , либо квадратными.

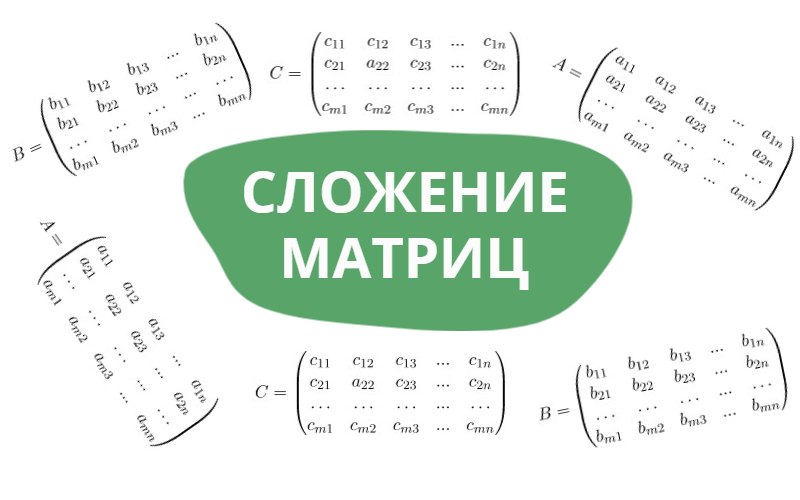
Итак, пусть нам даны матрицы

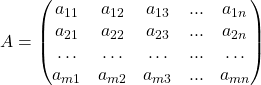
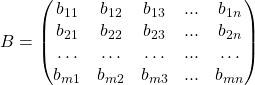
Тогда сумма матриц :

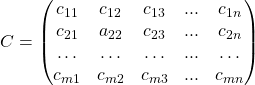
где , , , . , , , . , . .

Примеры сложения матриц

Пример 1

Сложите матрицы A и B, если:

Решение:

Матрицы A и B имеют одинаковое строение, значит мы можем их сложить, получим матрицу С:

Пример 2

Сложить матрицы A и B, если:

Решение:

Матрицы A и B сложить нельзя, так как матрица A — это матрица , а матрица B — это матрица , а мы можем складывать только прямоугольные матрицы одного порядка.

Пример 3

Сложить матрицы A и B, если:

Решение: матрицы имеют одинаковое прямоугольное строение, значит, их можно сложить:

Свойства сложения матриц

Так как при сложении матриц мы в основном складываем числа, то и свойства сложения чисел распространяются и на сложение матриц:

Противоположная матрица

Противоположной матрицей называется матрица, в которой все элементы заменены на противоположные относительно нуля.

Не путайте противоположную матрицу с обратной матрицей. Это разные матрицы.

Например, давайте найдем матрицу , противоположную матрице :

,

Очевидно, что это будет матрица:

Соответственно при сложении матриц мы получим нулевую матрицу:

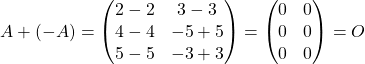
Вычитание матриц

Так как любое вычитание можно заменить сложением, то вычитание матриц можно заменить сложением матриц, например, вычитание из матрицы A матрицы B: это есть сложение матрицы A и матрицы, противоположной матрице B: .

Рассмотрим на примере: пусть нам нужно вычислить разность матриц

Находим разность этих матриц, как сложение матрицы A и матрицы, противоположной матрице B:

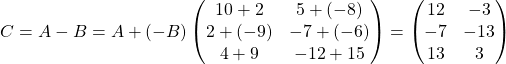
На примере видно, что разность двух матриц — это матрица, элементы которой получены путем вычитания из соответствующих элементов первой матрицы соответствующих элементов второй матрицы.

Основные операции над матрицами (сложение, умножение, транспонирование) и их свойства.

В этой теме будут рассмотрены такие операции, как сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы. Все обозначения, которые используются на данной странице, взяты из предыдущей темы «Матрицы. Виды матриц. Основные термины».

Сложение и вычитание матриц.

Аналогичное определение вводят и для разности матриц:

Запись «$i=overline$» означает, что параметр $i$ изменяется от 1 до m. Например, запись $i=overline$ говорит о том, что параметр $i$ принимает значения 1, 2, 3, 4, 5.

Стоит обратить внимание, что операции сложения и вычитания определены только для матриц одинакового размера. Вообще, сложение и вычитание матриц – операции, ясные интуитивно, ибо означают они, по сути, всего лишь суммирование или вычитание соответствующих элементов.

Заданы три матрицы:

Можно ли найти матрицу $A+F$? Найти матрицы $C$ и $D$, если $C=A+B$ и $D=A-B$.

Матрица $A$ содержит 2 строки и 3 столбца (иными словами – размер матрицы $A$ равен $2times 3$), а матрица $F$ содержит 2 строки и 2 столбца. Размеры матрицы $A$ и $F$ не совпадают, поэтому сложить их мы не можем, т.е. операция $A+F$ для данных матриц не определена.

Размеры матриц $A$ и $B$ совпадают, т.е. данные матрицы содержат равное количество строк и столбцов, поэтому к ним применима операция сложения.

$$ C=A+B=left(begin -1 & -2 & 1 \ 5 & 9 & -8 end right)+ left(begin 10 & -25 & 98 \ 3 & 0 & -14 end right)=\= left(begin -1+10 & -2+(-25) & 1+98 \ 5+3 & 9+0 & -8+(-14) end right)= left(begin 9 & -27 & 99 \ 8 & 9 & -22 end right) $$

Найдем матрицу $D=A-B$:

$$ D=A-B=left(begin -1 & -2 & 1 \ 5 & 9 & -8 end right)- left(begin 10 & -25 & 98 \ 3 & 0 & -14 end right)=\= left(begin -1-10 & -2-(-25) & 1-98 \ 5-3 & 9-0 & -8-(-14) end right)= left(begin -11 & 23 & -97 \ 2 & 9 & 6 end right) $$

Ответ: $C=left(begin 9 & -27 & 99 \ 8 & 9 & -22 end right)$, $D=left(begin -11 & 23 & -97 \ 2 & 9 & 6 end right)$.

Умножение матрицы на число.

Произведением матрицы $A_=(a_)$ на число $alpha$ называется матрица $B_=(b_)$, где $b_=alphacdot a_$ для всех $i=overline$ и $j=overline$.

Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.

Задана матрица: $ A=left(begin -1 & -2 & 7 \ 4 & 9 & 0 end right)$. Найти матрицы $3cdot A$, $-5cdot A$ и $-A$.

$$ 3cdot A=3cdot left(begin -1 & -2 & 7 \ 4 & 9 & 0 end right) =left(begin 3cdot(-1) & 3cdot(-2) & 3cdot 7 \ 3cdot 4 & 3cdot 9 & 3cdot 0 end right)= left(begin -3 & -6 & 21 \ 12& 27 & 0 end right).\ -5cdot A=-5cdot left(begin -1 & -2 & 7 \ 4 & 9 & 0 end right) =left(begin -5cdot(-1) & -5cdot(-2) & -5cdot 7 \ -5cdot 4 & -5cdot 9 & -5cdot 0 end right)= left(begin 5 & 10 & -35 \ -20 & -45 & 0 end right). $$

Запись $-A$ есть сокращенная запись для $-1cdot A$. Т.е., чтобы найти $-A$ нужно все элементы матрицы $A$ умножить на (-1). По сути, это означает, что знак всех элементов матрицы $A$ изменится на противоположный:

$$ -A=-1cdot A=-1cdot left(begin -1 & -2 & 7 \ 4 & 9 & 0 end right)= left(begin 1 & 2 & -7 \ -4 & -9 & 0 end right) $$

Произведение двух матриц.

Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.

Произведением матрицы $A_=(a_)$ на матрицу $B_=(b_)$ называется матрица $C_=(c_)$, для которой каждый элемент $c_$ равен сумме произведений соответствующих элементов i-й строки матрицы $A$ на элементы j-го столбца матрицы $B$: $$c_=sumlimits_^a_b_, ;; i=overline, j=overline.$$

Пошагово умножение матриц разберем на примере. Однако сразу стоит обратить внимание, что перемножать можно не все матрицы. Если мы хотим умножить матрицу $A$ на матрицу $B$, то сперва нужно убедиться, что количество столбцов матрицы $A$ равно количеству строк матрицы $B$ (такие матрицы часто называют согласованными). Например, матрицу $A_$ (матрица содержит 5 строк и 4 столбца), нельзя умножать на матрицу $F_$ (9 строк и 8 столбцов), так как количество столбцов матрицы $A$ не равно количеству строк матрицы $F$, т.е. $4neq 9$. А вот умножить матрицу $A_$ на матрицу $B_$ можно, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. При этом результатом умножения матриц $A_$ и $B_$ будет матрица $C_$, содержащая 5 строк и 9 столбцов:

Заданы матрицы: $ A=left(begin -1 & 2 & -3 & 0 \ 5 & 4 & -2 & 1 \ -8 & 11 & -10 & -5 end right)$ и $ B=left(begin -9 & 3 \ 6 & 20 \ 7 & 0 \ 12 & -4 end right)$. Найти матрицу $C=Acdot B$.

Для начала сразу определим размер матрицы $C$. Так как матрица $A$ имеет размер $3times 4$, а матрица $B$ имеет размер $4times 2$, то размер матрицы $C$ таков: $3times 2$:

Итак, в результате произведения матриц $A$ и $B$ мы должны получить матрицу $C$, состоящую из трёх строк и двух столбцов: $ C=left(begin c_ & c_ \ c_ & c_ \ c_ & c_ end right)$. Если обозначения элементов вызывают вопросы, то можно глянуть предыдущую тему: «Матрицы. Виды матриц. Основные термины», в начале которой поясняется обозначение элементов матрицы. Наша цель: найти значения всех элементов матрицы $C$.

Начнем с элемента $c_$. Чтобы получить элемент $c_$ нужно найти сумму произведений элементов первой строки матрицы $A$ и первого столбца матрицы $B$:

Чтобы найти сам элемент $c_$ нужно перемножить элементы первой строки матрицы $A$ на соответствующие элементы первого столбца матрицы $B$, т.е. первый элемент на первый, второй на второй, третий на третий, четвертый на четвертый. Полученные результаты суммируем:

$$ c_=-1cdot (-9)+2cdot 6+(-3)cdot 7 + 0cdot 12=0. $$

Продолжим решение и найдем $c_$. Для этого придётся перемножить элементы первой строки матрицы $A$ и второго столбца матрицы $B$:

Аналогично предыдущему, имеем:

$$ c_=-1cdot 3+2cdot 20+(-3)cdot 0 + 0cdot (-4)=37. $$

Все элементы первой строки матрицы $C$ найдены. Переходим ко второй строке, которую начинает элемент $c_$. Чтобы его найти придётся перемножить элементы второй строки матрицы $A$ и первого столбца матрицы $B$:

Следующий элемент $c_$ находим, перемножая элементы второй строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:

$$ c_=5cdot 3+4cdot 20+(-2)cdot 0 + 1cdot (-4)=91. $$

Чтобы найти $c_$ перемножим элементы третьей строки матрицы $A$ на элементы первого столбца матрицы $B$:

$$ c_=-8cdot (-9)+11cdot 6+(-10)cdot 7 + (-5)cdot 12=8. $$

И, наконец, для нахождения элемента $c_$ придется перемножить элементы третьей строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:

$$ c_=-8cdot 3+11cdot 20+(-10)cdot 0 + (-5)cdot (-4)=216. $$

Все элементы матрицы $C$ найдены, осталось лишь записать, что $C=left(begin 0 & 37 \ -23 & 91 \ 8 & 216 end right)$. Или, если уж писать полностью:

$$ C=Acdot B =left(begin -1 & 2 & -3 & 0 \ 5 & 4 & -2 & 1 \ -8 & 11 & -10 & -5 end right)cdot left(begin -9 & 3 \ 6 & 20 \ 7 & 0 \ 12 & -4 end right)=left(begin 0 & 37 \ -23 & 91 \ 8 & 216 end right). $$

Ответ: $C=left(begin 0 & 37 \ -23 & 91 \ 8 & 216 end right)$.

Кстати сказать, зачастую нет резона расписывать подробно нахождение каждого элемента матрицы-результата. Для матриц, размер которых невелик, можно поступать и так:

$$ left(begin 6 & 3 \ -17 & -2 endright)cdot left(begin 4 & 9 \ -6 & 90 end right) =left(begin 6cdot+3cdot(-6) & 6cdot+3cdot \ -17cdot+(-2)cdot(-6) & -17cdot+(-2)cdot end right) =left(begin 6 & 324 \ -56 & -333 end right) $$

Стоит также обратить внимание, что умножение матриц некоммутативно. Это означает, что в общем случае $Acdot Bneq Bcdot A$. Лишь для некоторых типов матриц, которые именуют перестановочными (или коммутирующими), верно равенство $Acdot B=Bcdot A$. Именно исходя из некоммутативности умножения, требуется указывать как именно мы домножаем выражение на ту или иную матрицу: справа или слева. Например, фраза «домножим обе части равенства $3E-F=Y$ на матрицу $A$ справа» означает, что требуется получить такое равенство: $(3E-F)cdot A=Ycdot A$.

Транспонированная матрица.

Транспонированной по отношению к матрице $A_=(a_)$ называется матрица $A_^=(a_^)$, для элементов которой $a_^=a_$.

Попросту говоря, для того, чтобы получить транспонированную матрицу $A^T$, нужно в исходной матрице $A$ заменить столбцы соответствующими строками по такому принципу: была первая строка – станет первый столбец; была вторая строка – станет второй столбец; была третья строка – станет третий столбец и так далее. Например, найдем транспонированную матрицу к матрице $A_$:

Соответственно, если исходная матрица имела размер $3times 5$, то транспонированная матрица имеет размер $5times 3$.

Некоторые свойства операций над матрицами.

Здесь предполагается, что $alpha$, $beta$ – некоторые числа, а $A$, $B$, $C$ – матрицы. Для первых четырех свойств я указал названия, остальные можно назвать по аналогии с первыми четырьмя.

1. $A+B=B+A$ (коммутативность сложения)
2. $A+(B+C)=(A+B)+C$ (ассоциативность сложения)
3. $(alpha+beta)cdot A=alpha A+beta A$ (дистрибутивность умножения на матрицу относительно сложения чисел)
4. $alphacdot(A+B)=alpha A+alpha B$ (дистрибутивность умножения на число относительно сложения матриц)
5. $A(BC)=(AB)C$
6. $(alphabeta)A=alpha(beta A)$
7. $Acdot (B+C)=AB+AC$, $(B+C)cdot A=BA+CA$.
8. $Acdot E=A$, $Ecdot A=A$, где $E$ – единичная матрица соответствующего порядка.
9. $Acdot O=O$, $Ocdot A=O$, где $O$ – нулевая матрица соответствующего размера.
10. $left(A^T right)^T=A$
11. $(A+B)^T=A^T+B^T$
12. $(AB)^T=B^Tcdot A^T$
13. $left(alpha A right)^T=alpha A^T$

В следующей части будет рассмотрена операция возведения матрицы в целую неотрицательную степень, а также решены примеры, в которых потребуется выполнение нескольких операций над матрицами.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Сложение матриц / Сумма матриц онлайн

Суммой матриц $A$ и $B$ одного размера называется матрица $C = A+B$ такого же размера, получаемая из исходных путем сложения соответствующих элементов: $$ A_+B_=C_ ; c_=a_+b_, i=overline, j=overline $$

Складывать можно только матрицы одинакового размера.

Свойства сложения и вычитания матриц:

1. Ассоциативность $ (A+B)+C=A+(B+C) $
2. $ A+Theta=Theta+A $, где $Theta$ — нулевая матрица соответствующего размера.
3. $ A-A=Theta $
4. Коммутативность $ A+B=B+A $

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + — * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: ^T
• Возведение в целую степень: ^

Примеры корректных выражений

• Cложение двух матриц: A+B , (A)+(B) , ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A — 0.5B)^5
• Произведение транспонированной матрицы на исходную: A^TA
• Обратная матрица в квадрате для B: B^-2

Видео

Свойства

1. Если матрицы $ A,B,C $ одинаковые по размеру, тогда для них действует свойство ассоциативности: $$ A + (B + C) = (A + B) + C $$
2. Для каждой матрицы существует нулевая матрица, обозначаемая $ O $, при сложении (вычитании) с которой исходная матрица не изменяется: $$ A pm O = A $$
3. Для каждой ненулевой матрицы $ A $ есть противоположная матрица $ (-A) $ сумма с которой обращается в нуль: $$ A + (-A) = 0 $$
4. При сложении (вычитании) матриц допустимо свойство коммутативности, то есть матрицы $ A $ и $ B $ можно менять местами: $$ A + B = B + A $$ $$ A — B = B — A $$

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби ( 1/2 , 29/7 , -1/125 ), десятичные дроби ( 12 , -0.01 , 3.14 ), а также числа в экспоненциальной форме ( 2.5e3 , 1e-2 ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки ( ← , ↑ , → , ↓ ) для перемещения по элементам

Сложение матриц онлайн-калькулятором

Изучение матриц и выполнение заданий, связанных с ними, актуально для студентов технических специальностей. Чтобы найти сумму матриц онлайн-калькулятором, вам потребуется только ввести значения в пустые поля и дождаться автоматического вычисления результата. Так вы сможете свериться с собственным решением, полученным при самостоятельных расчетах. Сложение и вычитание матриц онлайн-калькулятором понадобится дляподготовки к занятиям. Подробное готовое решение помогает понять алгоритм, который лежит в основе вычислений, и применять его в дальнейшем. Сервис пригодится и для преподавателей математики, так как позволит сэкономить время при проверке студенческих работ.

Нахождение суммы или разности матриц онлайн-калькулятором предполагает:

• Выбор размера матриц (необходимо задать количество строк и столбцов);
• Введение значений матрицы и множителей в пустые графы;
• Отправку примера на вычисление — поочередное перемножение и сложение (вычитание) элементов матрицы, упрощение выражения;
• Получение ответа.

Кроме вычитания и сложения матриц онлайн наш сервис предлагает использование других калькуляторов. Если вам необходима помощь профессионального преподавателя в решении задачи, напишите консультанту на сайте. Сотрудник компании ответит на интересующие вопросы, оформит заказ и предоставит скидку.

Сложение матриц и его свойства

2.1.1. Определение. Суммой матриц A=(a_ij)_m´n и B=(b_ij)_m´n называется матрица (a_ij+b_ij)_m´n.

Сумма матриц A и B обозначается через A+B.

Таким образом, по определению (a_ij)_m´n+(b_ij)_m´n=(a_ij+b_ij)_m´n, можно складывать только матрицы одинаковой размерности и при сложении матриц складываются соответствующие элементы матриц. Например,

2.1.2. Теорема. Операция сложения матриц обладает следующими свойствами:

1 о . A+B=B+A.

2 о . (A+B)+C=A+(B+C).

3 о . A_m´n+O_m´n=A_m´n.

4 о . Для любой матрицы A_m´n существует матрица B_m´n такая, что A+B=O_m´n.

Матрица B называется противоположной к A и обозначается через —A. Очевидно, —A=(-a_ij)_m´n.

2.1.3. Свойство 2 о имеет обобщение: результат суммирования нескольких матриц

(…((A₁+A₂)+A₃)+…+A_k—1)+A_k (2.1)

не зависит от расстановки скобок, то есть

(…((A₁+A₂)+A₃)+…+A_k—1)+A_k=((A₁+A₂)+(A₃+A₄))+…+A_k

и т.д. Поэтому в суммах вида (2.1) скобки принято опускать: A₁+A₂+…+A_k.

2.1.4. Определение. Сумма A+(-B) называется разностью матриц A и B и обозначается через A—B: A+(-B)=A—B.

Ясно, что если A=(a_ij)_m´n, B=(b_ij)_m´n, то A—B=(a_ij—b_ij)_m´n, то есть для получения разности матриц A и B нужно из элементов матрицы A вычесть соответствующие элементы матрицы B. Например,

Сложение матриц

Суммой матриц , имеющих строк и столбцов, называется матрица элементы которой равны сумме соответствующих элементов этих матриц, причём .

Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.

Отметим, что сложение, матриц определено только тогда, когда матрица имеет одинаковое число строк и столбцов с матрицей .

Пусть даны две квадратные матрицы:

Произведением двух матриц называется третья матрица

элементы которой определяются следующим образом:

т. е. элемент матрицы есть сумма произведений элементов -й строки матрицы на элементы -гo столбца матрицы .

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Аналогично определяется произведение неквадратных матриц, причём допускает умножение на матрицу и дает произведение в том и только том случае, когда число столбцов матрицы совпадает с числом строк матрицы к при этом несущественно, сколько строк имеет матрица и сколько столбцов имеет матрица . Произведение имеет одинаковое число строк с матрицей и одинаковое число столбцов с матрицей ,

Добавление матриц A и B является арифметической операцией, поэтому нам нужно получить матрицу C, каждый элемент которой равен сумме соответствующих элементов добавленной матрицы.

Пример:

Таким образом, в общем случае . Отметим, что

т.е. определитель произведения двух квадратных матриц -го порядка равен произведению определителей перемножаемых матриц- и

В этом случае произведение не определено, поскольку число столбцов в матрице не равно числу строк в матрице .

Возможно вам будут полезны данные страницы:

Отметим» что если существуют лве матрицы и , для которых . то они квадратные.

г) Показать, что

Сложение матриц

Пусть А и В — матрицы одинаковых размеров (т. е. состоящие из одинакового числа строк и одинакового числа столбцов),

называется суммой матриц А и В, если ее элементы вычисляются по правилу

Иными словами, складываются элементы матриц А и В, стоящие в одинаковых позициях (в -й строке и в -м столбце), и полученная сумма записывается в новой матрице С в ту же позицию (г, к). Это можно записать и так:

Обозначение: А + В.

Вычитание матриц определяется аналогично.

Замечание. Операция сложения определена лишь для матриц, имеющих одинаковые размеры. Если матрицы имеют разное число строк или разное число столбцов, то складывать их нельзя.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.

Похожие записи:

• 

  Что такое супер аон на билайн

• 

  Что такое сумма чисел и разность 1 класс

• 

  Что такое сумма чисел и разность чисел в математике…

• 

  Что такое супер амолед в смартфоне

• 

  Что такое супер амолед дисплей

• 

  Что такое сумма определение